O movimento circular uniforme (UCM) é um conceito fundamental em cinemática que descreve um tipo específico de movimento no qual um objeto se move em torno de um ponto fixo em uma trajetória circular a uma velocidade constante.
Neste artigo definiremos o MCU, e os diferentes conceitos básicos relacionados a este movimento, alguns exemplos reais que ilustram este movimento, as fórmulas para seu cálculo e resolveremos alguns exercícios para melhor compreendê-lo.
Definição de movimento circular uniforme (MCU)
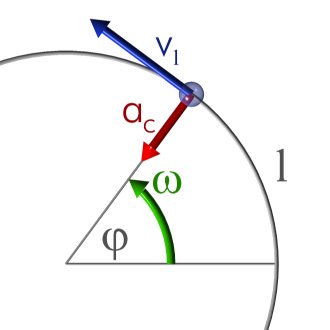O movimento circular uniforme (UCM) é um tipo específico de movimento no qual um objeto se move em torno de um ponto fixo em um caminho circular a uma velocidade constante.
No MCU, a velocidade do objeto permanece inalterada em magnitude e direção ao longo de seu caminho, o que significa que a velocidade angular é constante.
O movimento circular uniforme é caracterizado pela relação entre a velocidade angular e a velocidade linear, que está diretamente relacionada ao raio da trajetória circular.
Este movimento é normalmente observado em situações como a órbita de um planeta em torno de uma estrela, o giro de uma roda em um veículo em movimento ou mesmo em parques de diversões em montanhas-russas, onde os passageiros experimentam uma sensação constante de velocidade e direção enquanto giram. um ponto central.
Noções básicas de MCU
Para entender o MCU, é essencial se familiarizar com alguns conceitos-chave:
1. Período (T) e frequência (f)
O período (T) é o tempo que leva para o objeto completar uma revolução completa em torno da trajetória circular. A frequência (f) é o número de revoluções que o objeto completa em um segundo. Eles estão relacionados da seguinte forma:
f = 1/T
No Sistema Internacional de Unidades (SI), o período é medido em segundos (s). Por outro lado, a frequência é medida em hertz (Hz). Um hertz é igual a um ciclo por segundo.
2. Velocidade angular (ω)
A velocidade angular (ω) é uma medida de quão rápido o objeto está se movendo em um caminho circular. É medido em radianos por segundo (rad/s) e está relacionado à frequência (f) da seguinte forma:
ω = 2·π·f
3. Raio do caminho (r)
O raio do caminho (r) é a distância do ponto central ao objeto em movimento no MCU. Este valor é constante durante todo o movimento.
4. Velocidade linear (v)
Velocidade linear (v) é a velocidade com a qual o objeto se move tangencialmente ao longo do caminho circular. Por esse motivo também é conhecida como velocidade tangencial.
A velocidade tangencial está relacionada à velocidade angular (ω) e ao raio (r) da seguinte forma:
v = r·ω
5. Aceleração centrípeta (ac)
A aceleração centrípeta (ac) é uma aceleração fictícia que atua sobre o objeto na direção oposta ao centro da trajetória circular. Sua magnitude está relacionada à velocidade angular (ω) e ao raio (r) da seguinte forma:
a c =r·ω 2
As unidades de aceleração centrípeta são metros por segundo ao quadrado (m/s²).
Fórmulas para movimento circular uniforme
As fórmulas a seguir são essenciais para compreender e resolver problemas relacionados ao MCU:
-
Relação entre velocidade angular e velocidade linear: v=rω
-
Relação entre período e frequência:T=1/f
-
Relação entre velocidade angular e frequência: ω=2πf
-
Relação entre aceleração centrípeta, velocidade angular e raio: a c =rω2
Exemplos na vida cotidiana
O movimento circular uniforme é encontrado em vários aspectos da vida cotidiana.
-
Turbinas a vapor em usinas nucleares: Turbinas a vapor em usinas nucleares utilizam o MCU para converter energia térmica em energia mecânica, gerando eletricidade.
-
Ventiladores de teto: As pás do ventilador de teto funcionam como um MCU para circular o ar uniformemente em uma sala, proporcionando resfriamento.
-
Veículos em curvas: Os veículos, ao fazerem curvas circulares, seguem um MCU que pode ser calculado através destas fórmulas.
-
Fabricação de corda: Torcer uma corda para criar uma corda envolve um MCU, onde a corda é enrolada uniformemente em torno de um núcleo central.
Exercícios resolvidos
Agora, vamos resolver alguns exercícios típicos relacionados ao MCU:
Exercício 1
Suponha que um carro de corrida se mova com velocidade constante de 100 m/s em torno de uma pista circular com raio de 200 metros. Calcule o período, a frequência e a velocidade angular do movimento.
Solução:
Como a velocidade é constante, podemos usar a fórmula da velocidade angular:
v = r·ω
Substituindo valores conhecidos:
100m/s = 200m ⋅ω
Para encontrar ω:
ω = (100 m/s) / 200 m=0,5 rad/s
Agora, podemos encontrar o período (T) usando a relação entre velocidade angular e frequência:
ω = 2·π·f
0,5 rad/s = 2·π⋅f
Para encontrar f:
f = (0,5 rad/s) / (2·π) ≈ 0,0796 Hz
E finalmente, o período (T) é o inverso da frequência:
T = 1/f ≈ 12,57s
Exercício 2
Um objeto se move ao longo de uma trajetória circular de raio 4 metros a uma velocidade angular de 2 radianos por segundo. Calcule sua velocidade linear e aceleração centrípeta.
Solução:
Para encontrar a velocidade linear, usamos a fórmula:
v = r·ω
Substituindo valores conhecidos:
v = 4 m ⋅ 2 rad/s = 8 m/s
Para aceleração centrípeta, usamos a fórmula:
ac = r·ω 2
Substituindo valores conhecidos:
ac =4 m⋅(2 rad/s)2=16 m/s 2
