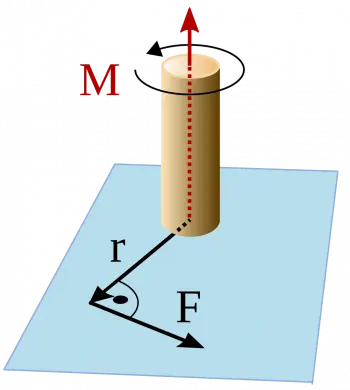
O momento de uma força, também conhecido como "torque", é uma quantidade física que mede a tendência de uma força de girar um objeto em torno de um ponto ou eixo de rotação.
O momento de uma força está relacionado às leis de Newton porque a magnitude da força aplicada afeta a aceleração angular do objeto (segunda lei) e porque o momento gerado pela força em um objeto também gera uma força igual, mas oposta no objeto. direção do eixo de rotação ou em outro objeto (terceira lei).
Matematicamente, o momento de uma força é definido como o produto do valor da força (F) e a distância perpendicular (r) do ponto de aplicação da força ao eixo de rotação.
O momento de uma força pode ser calculado em diferentes situações, seja no contexto de um objeto em repouso (estático) ou em movimento (dinâmico).
Fórmula para o momento de uma força
A fórmula para calcular o momento (τ) de uma força (F) em relação a um ponto ou eixo de rotação, levando em consideração a distância perpendicular (r) do ponto de aplicação da força ao eixo de rotação, é como segue:
Momento (τ) = F × r
Onde:
-
τ = Momento da força (torque) em unidades de newton metros (Nm) ou libras-pé (lb-ft)
-
F = Magnitude da força aplicada, medida em newtons (N) ou libras (lb)
-
r = Distância perpendicular do ponto de aplicação da força ao eixo de rotação, medida em metros (m) ou pés (ft)
Esta fórmula se aplica quando a força e a distância são perpendiculares entre si, o que significa que a força atua em uma direção que faz um ângulo de 90 graus com o raio ou distância do eixo de rotação.
Nas situações em que a força e a distância não são perpendiculares, é necessário usar conceitos de vetores ou trigonometria para decompor a força em suas componentes perpendiculares ao raio, o que permitirá calcular o momento resultante.
Se feito em termos de vetores, a direção do momento segue a regra da mão direita ou a regra do saca-rolhas, dependendo da convenção. Isso implica que o momento pode ser positivo ou negativo, dependendo da direção em que a força atua em relação ao eixo de rotação.
Exemplos
O momento de uma força tem aplicações comuns em nosso cotidiano em diversas situações. Aqui estão alguns exemplos de como o momento de uma força é aplicado no dia a dia:
-
Abrindo Portas: Quando você gira a maçaneta de uma porta para abri-la, está aplicando um momento nas dobradiças. Quanto mais longe das dobradiças estiver a força aplicada, mais fácil será abrir a porta, pois o momento aumentará e será necessária menos força para girar.
-
Parafusos de aperto: Quando você usa uma chave para apertar um parafuso, aplica um momento sobre o eixo do parafuso. O comprimento da chave (distância do eixo do parafuso) influencia a quantidade de força que você precisa aplicar para apertar o parafuso com sucesso.
-
Girando uma chave: Quando você usa uma chave para afrouxar ou apertar porcas e parafusos, está aplicando um momento sobre o eixo do parafuso. Novamente, o comprimento da chave determina a quantidade de momento gerado e, portanto, a facilidade de girar a porca ou o parafuso.
-
Volante de carro: quando você gira o volante de um carro para mudar de direção, aplica um momento sobre o eixo de direção do veículo. Quanto mais você virar o volante do eixo de direção, mais rápido a direção do carro mudará.
-
Balançando em um balanço: Ao balançar, você aplica impulso ao redor dos ganchos do balanço. Ao empurrar os pés para frente e para trás enquanto está sentado no balanço, você controla o impulso e determina o alcance e a velocidade do movimento.
-
Bicicleta: ao aplicar uma força nos pedais de uma bicicleta, gera um momento de forças em relação ao eixo dos pedais. Da mesma forma, a força transmitida à corrente depende diretamente do raio das coroas, que é a distância do centro de rotação.
-
Alavanca: Uma alavanca é uma máquina simples que consiste em uma barra rígida que gira em torno de um ponto fixo chamado fulcro. Ao aplicar uma força em uma extremidade da alavanca (força de entrada), é gerado um momento que permite levantar uma carga na outra extremidade (força de saída).
-
Polia: Uma polia é uma roda com uma corda ou cabo passando por ela. Puxar uma extremidade da corda (força de entrada) aplica um momento na polia, permitindo que uma carga seja levantada na outra extremidade (força de saída).
-
Turbina a vapor: as turbinas a vapor utilizadas nos geradores elétricos de uma usina nuclear são projetadas para que o vapor gere uma força tangencial à roda e perpendicular ao eixo de tal forma que gere um momento de forças para obter um movimento circular .
Exercícios resolvidos
Exercício 1: Momento de uma força perpendicular ao eixo de rotação
Suponha que temos uma porta que gira em torno de suas dobradiças e aplicamos uma força de 20 newtons na direção perpendicular ao eixo de rotação, a uma distância de 0,5 metros do eixo de rotação ao ponto de aplicação da força. Calcule o momento da força.
Solução
O momento da força seria calculado da seguinte forma:
Momento (τ) = F × r
τ = 20 N × 0,5 m
τ = 10 Nm
O momento da força aplicada à porta é de 10 newton metros (Nm).
Exercício 2: Momento de uma força não perpendicular ao eixo de rotação
Agora suponha que aplicamos uma força de 30 newtons na mesma porta, mas desta vez a força atua em um ângulo de 60 graus em relação ao eixo de rotação, e a distância do eixo de rotação ao ponto de aplicação da força é 1 metro. Calcule o momento da força.
Solução
Para calcular o momento, devemos primeiro decompor a força em seus componentes perpendiculares ao raio.
Força perpendicular ao raio (Fperpendicular ) = F × cos(θ)
Fperpendicular = 30 N × cos(60°)
Fperpendicular = 30 N × 0,5
Fperpendicular = 15 N
Momento (τ) = Fperpendicular × r
τ = 15 N × 1 m
τ = 15 Nm
O momento da força aplicada na porta, considerando sua componente perpendicular ao raio, é de 15 newton metros (Nm).
