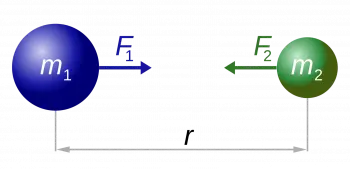
A Lei da Gravitação Universal de Newton é um dos pilares fundamentais da física e foi desenvolvida por Sir Isaac Newton no século XVII. Esta lei descreve a força de atração entre dois corpos devido à sua massa e distância relativa.
É uma das leis mais importantes e amplamente aplicadas no campo da física clássica e tornou possível entender e prever muitos fenômenos no universo.
Neste artigo, vamos explorar em detalhes o que é a Lei da Gravitação Universal, sua fórmula, sua importância e alguns exemplos que ilustram sua aplicação.
O que é a Lei da Gravitação Universal?
A Lei da Gravitação Universal estabelece que a força de atração entre dois corpos é diretamente proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância que os separa.
Ou seja, quanto maior a massa dos objetos e quanto mais próximos estiverem uns dos outros, maior será a força de atração gravitacional entre eles.
A fórmula da Lei da Gravitação Universal:
A fórmula matemática para calcular a força gravitacional entre dois objetos é expressa da seguinte forma:
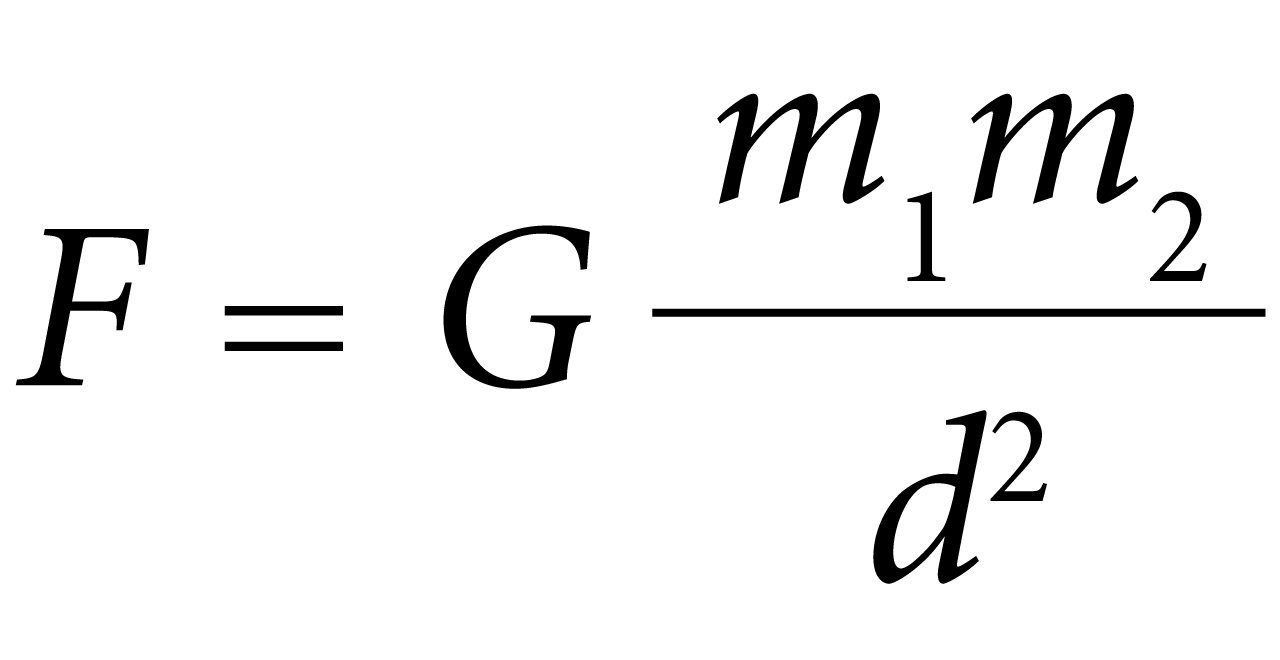
Onde:
-
F é a força gravitacional entre objetos expressa em newtons,
-
G é a constante gravitacional universal, aproximadamente 6,674 × 10 -11 N (m/kg) 2
-
m 1 e m 2 são as massas dos objetos expressas em quilogramas (kg).
-
r é a distância entre os centros de massa dos objetos expressa em metros (m).
A constante gravitacional universal (G) tem valor aproximado de 6,674 × 10 -11 N (m/kg) 2 e é utilizada para dimensionar a força de atração em função das unidades de massa e distância utilizadas.
Importância da Lei da Gravitação Universal:
A Lei da Gravitação Universal é de extrema importância no estudo e compreensão do universo. Por meio dessa lei, podemos explicar e prever fenômenos como a órbita dos planetas ao redor do Sol, os movimentos das luas ao redor dos planetas e a interação entre objetos massivos no espaço.
Além disso, a lei também tem aplicações práticas na vida cotidiana. Por exemplo, permite entender o funcionamento de satélites artificiais que orbitam a Terra e é essencial para a navegação espacial e o planejamento de missões espaciais.
Exemplos de aplicação da Lei da Gravitação Universal:
Abaixo mostramos 4 exemplos em que a lei da gravitação universal de Newton é aplicada:
1. A órbita da Terra em torno do Sol
A força gravitacional entre a Terra e o Sol é responsável por manter nosso planeta em uma órbita estável em torno da estrela.
Essa força permite que a Terra se mantenha em movimento circular ao redor do Sol e determina o período de um ano. A força que o Sol exerce sobre a Terra é perpendicular à velocidade linear da Terra em cada momento.
2. A Lua e as marés
A força gravitacional entre a Terra e a Lua é responsável pelas marés. A Lua exerce uma força de atração sobre os oceanos, fazendo com que o nível da água suba e desça conforme a Terra gira.
Como o Sol e a Terra, essa força é a força centrípeta que força a Lua a orbitar a Terra.
3. Satélites artificiais
No projeto e operação de satélites artificiais, os cálculos também são feitos usando a fórmula da lei da gravitação universal.
Para manter um satélite em órbita, uma velocidade e altitude específicas são necessárias para equilibrar a força gravitacional com a força centrífuga gerada pelo movimento orbital.
4. Queda de objetos
A lei também se aplica a objetos em queda na superfície da Terra. Quanto maior a massa do objeto, maior a força gravitacional agindo sobre ele e mais rápido ele cairá.
Exercícios da lei da gravitação universal
Abaixo mostramos três exercícios resolvidos que ilustram a aplicação desta lei da física:
Exercício 1: Calculando a força gravitacional entre dois corpos
Suponha que temos dois objetos: um com massa de 5 kg e outro com massa de 8 kg. A distância entre os centros de massa dos objetos é de 2 metros. Queremos calcular a força gravitacional entre eles.
Dados
-
m 1 = 5kg
-
m2 = 8kg
-
r=2m
-
G = 6,674 × 10 -11 N (m/kg) 2
Solução:
Usamos a fórmula da Lei da Gravitação Universal:
F = G (m 1 m 2 ) / r 2
Substituindo os valores conhecidos:
F = (6,674 × 10 -11 N (m/kg) 2 ) * (5 kg * 8 kg) / (2 m) 2
F = 6,674 × 10 -10 N
Portanto, a força gravitacional entre os dois corpos é de aproximadamente 6,674 × 10 -10 N.
Exercício 2: Calculando a força gravitacional entre a Terra e um objeto
Suponha que queremos calcular a força gravitacional entre a Terra (massa ≈ 5.972 × 1024 kg) e um objeto com massa de 100 kg. A distância entre o centro da Terra e o objeto é de 6,371 × 10^6 metros (raio aproximado da Terra).
Dados:
-
m 1 (massa da Terra) = 5,972 × 10 24 kg
-
m 2 (massa do objeto) = 100 kg
-
r (distância) = 6,371 × 10 6 m
-
G = 6,674 × 10 -11 N (m/kg) 2
Solução:
Aplicamos a fórmula da Lei da Gravitação Universal:
F = G (m 1 m 2 ) / r 2
Substituindo os valores conhecidos:
F = (6.674 × 10-11 N (m/kg) 2 ) * ((5.972 × 1024 kg) * (100 kg)) / (6.371 × 106 m)2
F = 981,95N
Portanto, a força gravitacional entre a Terra e o objeto é de aproximadamente 981,95 N.
Exercício 3: Calculando a massa de um objeto a partir da força gravitacional
Suponha que temos dois objetos e sabemos que a força gravitacional entre eles é de 100 N. A distância entre os objetos é de 10 metros e a massa de um dos objetos é de 5 kg. Queremos calcular a massa do segundo objeto.
Dados:
-
F = 100N
-
r = 10m
-
m 1 = 5kg
-
G = 6,674 × 10 -11 N (m/kg) 2
Solução:
Usamos a fórmula da Lei da Gravitação Universal e limpamos m2:
F = G (m 1 m 2 ) / r 2
Limpamos m2:
m 2 = (F * r 2 ) / (G * m 1 )
Substituindo os valores conhecidos:
m 2 = (100 N * (10 m) 2 ) / ((6,674 × 10 -11 N (m/kg) 2 ) * 5 kg)
m 2 ≈ 2,997 × 10 13 kg
Portanto, a massa do segundo objeto é de aproximadamente 2,997 × 10 13 kg.
